Portafolio De Inversion en Python

Este ejercicio se realiza bajo la guía del vídeo How to Invest with Data Science hecho por Derek Banas, el código es de su autoría, este es un ejercicio netamente académico y no busca ser una guía financiera.

Objetivo

Generar por medio de Python código que permita la extracción de datos de inversión bursátil, la selección de un conjunto de activos y la creación de un portafolio de inversión.

Datos

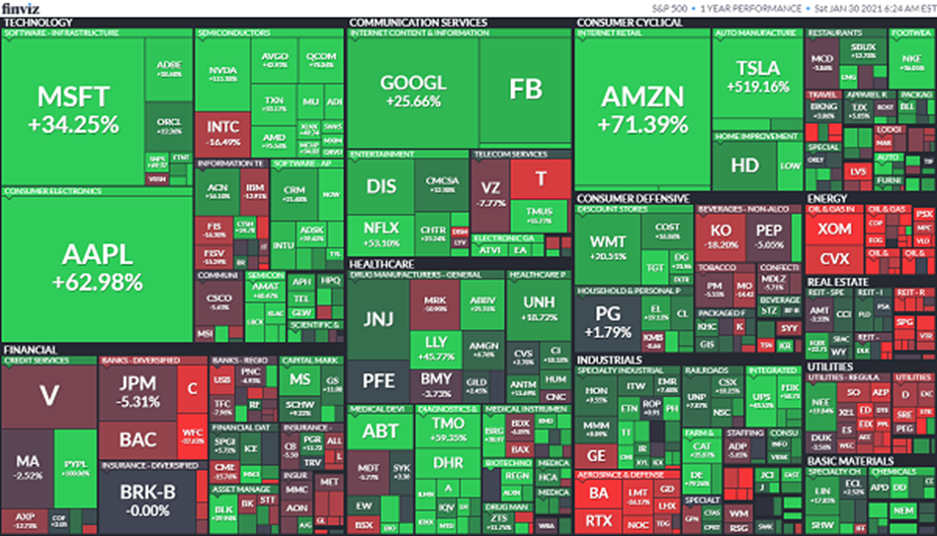
Los datos que vamos a utilizar son los de activos bursátiles que se encuentran en Yahoo Finance. Para este caso se trabajaran con el grupo de activos Wilshire 5000.

Wilshire 5000

Es un índice ponderado por la capitalización bursátil del valor de mercado de todas las acciones americanas negociadas activamente en Estados Unidos. El índice pretende medir el rendimiento de la mayoría de las empresas que cotizan en bolsa con sede en los Estados Unidos, con datos de precios fácilmente disponibles, (se excluyen las acciones del Bulletin Board/penny y las acciones de empresas extremadamente pequeñas).

Generación del portafolio

Se presenta a continuación un resúmen de las principales funcionalidades del código, para tener acceso a los archivos utilizar este link

1. Obtención de la información de las acciones. Archivo: Portafolio_inversion_descarga.py

Decarga o consulta de la información de acciones desde Yahoo Finance ##

# Definción de variables
PATH = 'E:\Estudio\Análisis de datos\Proyectos\Portafolio de inversión en python\Wilshire/'

# Fechas de inicio y finalización por defecto
S_DATE = '2017-02-01'
E_DATE = '2022-06-19'
S_DATE_DT = pd.to_datetime(S_DATE)
E_DATE_DT = pd.to_datetime(E_DATE)

Generación de una función para la obtención de los datos de columnas desde los CSV

def get_column_from_csv (file, col_name):
    try:
        df = pd.read_csv(file)
    except FileNotFoundError:
        print('Archivo no existe')
    else:
        return df[col_name]

Obtener la información del indicativo de las acciones de un archivo CSV previamente creado con los tickers

tickers = get_column_from_csv('E:\Estudio\Análisis de datos\Proyectos\Portafolio de inversión en python\Wilshire-5000-stocks.csv', 'Ticker')

Guardar los datos de las acciones en un CSV

# Creación de la función que genera un dataframe con el ticker y la fecha de inicio

def save_to_csv_from_yahoo(folder, ticker):
    stock = yf.Ticker(ticker)

    try:
        print('Obtener datos para: ', ticker)
        # Obtención de los datos historicos del precio de cierre
        df = stock.history(period='5y')

        # Espera de dos segundos
        time.sleep(2)

        # Remoción del punto para guardar el archivo CSV
        # Guardar os datos en un CSV
        # Guardado del archivo
        the_file = folder + ticker.replace('.','_')+'.csv'
        print(the_file, ' Guardado')
        df.to_csv(the_file)
    except Exception as ex:
        print('No se pudo obtener datos para: ', ticker)

Descarga de toda la información de las acciones

for x in range (0, 3481):
    save_to_csv_from_yahoo(PATH, tickers[x])
    print('Terminado')

Resultado:

Generación de archivos CSV con los datos consultados de los ticks establecidos, no se descargan para la totalidad de 3481 acciones, dado que los ticks han cambiado debido a fusiones o eliminaciones de empresas.

Los CSV contienen datos para cada una de las acciones de la fecha de lectura histórica (diaria), precio de abertura, precio máximo, precio mínimo, precio de cierre, dividendos generados, stock y splite.

2. Generación de cálculos requeridos para la creación de gráficos. Archivo: Portafolio_inversion_calculos.py

Obtener un listado de los stocks que han sido descargados

files = [x for x in listdir(PATH) if isfile(join(PATH, x))]
tickers = [os.path.splitext(x)[0] for x in files]

tickers.sort()
len(tickers)

Añadir una columna con los retornos diarios: precio de cierre de un día dividido en el anterior menos uno.

def add_daily_return_to_df (df):
    df['daily_return'] = df['Close']/df['Close'].shift(1) - 1
    return df

Añadir una columna con los retornos acumulados: acumulado del retorno diario para cada día

def add_cum_return_to_df (df):
    df['cum_return'] = (1 + df['daily_return']).cumprod() # cumprod()function is used when we want to compute the cumulative product of array elements over a given axis
    return df

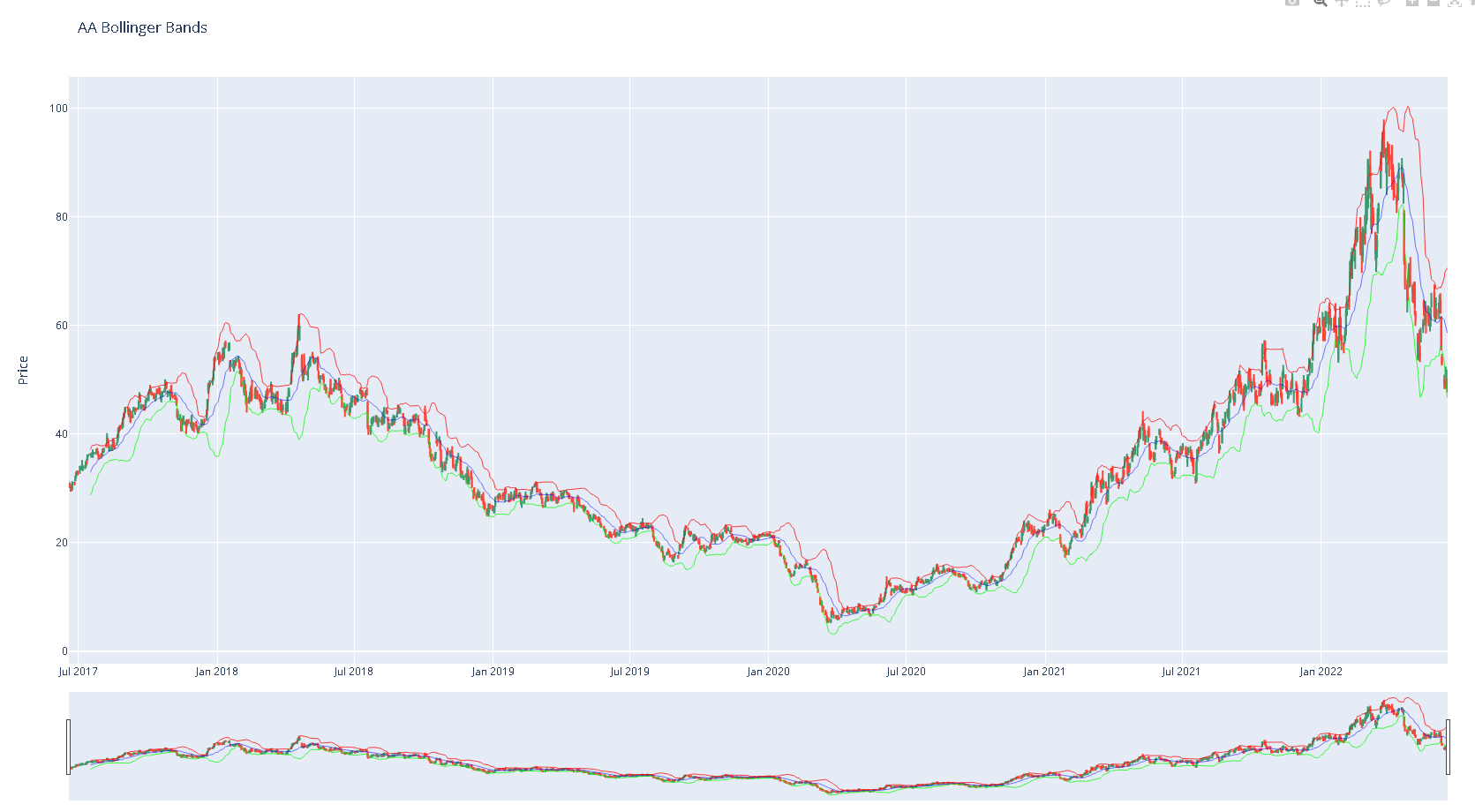
Añadir Bollinger bands

Bollinger Bands plot 2 lines using a moving average and the standard deviation defines how far apart the lines are. They also are used to define if prices are to high or low. When bands tighten it is believed a sharp price move in some direction. Prices tend to bounce off of the bands which provides potential market actions.

A strong trend should be noted if the price moves outside the band. If prices go over the resistance line it is in overbought territory and if it breaks through support it is a sign of an oversold position.

Definición de la función para las Bollinger bands

def add_bollinger_bands(df):
    # Generación de la banda central (promedio movil) del precio de cierre con una ventana de 20 días
    df['middle_band'] = df['Close'].rolling(window = 20).mean()
    # Generación de la banda superior con dos veces la desviación estándar
    df['upper_band'] = df['middle_band'] + 2*df['Close'].rolling(window = 20).std()
    # Generación de la banda inferior con dos veces menos la desviación estándar
    df['lower_band'] = df['middle_band'] - 2*df['Close'].rolling(window = 20).std()
    return df

Añadir los datos Ichimoku al df

The Ichimoku (One Look) is considered an all in one indicator. It provides information on momentum, support and resistance. It is made up of 5 lines. If you are a short term trader you create 1 minute or 6 hour. Long term traders focus on day or weekly data.

Conversion Line (Tenkan-sen) : Represents support, resistance and reversals. Used to measure short term trends. Baseline (Kijun-sen) : Represents support, resistance and confirms trend changes. Allows you to evaluate the strength of medium term trends. Called the baseline because it lags the price. Leading Span A (Senkou A) : Used to identify future areas of support and resistance Leading Span B (Senkou B) : Other line used to identify suture support and resistance Lagging Span (Chikou) : Shows possible support and resistance. It is used to confirm signals obtained from other lines. Cloud (Kumo) : Space between Span A and B. Represents the divergence in price evolution. Formulas

Lagging Span = Price shifted back 26 periods Base Line = (Highest Value in period + Lowest value in period)/2 (26 Sessions) Conversion Line = (Highest Value in period + Lowest value in period)/2 (9 Sessions) Leading Span A = (Conversion Value + Base Value)/2 Leading Span B = (Period high + Period low)/2 (52 Sessions)

def add_Ichimoku(df):
    # Conversion Line = (Highest Value in period + Lowest value in period)/2 (9 Sessions)
    hi_val = df['High'].rolling(window = 9).max()
    low_val = df['Low'].rolling(window = 9).min() 
    df['Conversion'] = (hi_val + low_val)/2

    # Base Line = (Highest Value in period + Lowest value in period)/2 (26 Sessions)
    hi_val2 = df['High'].rolling(window = 26).max()
    low_val2 = df['Low'].rolling(window = 26).min() 
    df['Baseline'] = (hi_val2 + low_val2)/2

    # Leading Span A = (Conversion Value + Base Value)/2
    df['SpanA'] = ((df['Conversion'] + df['Baseline'])/2)

    # Leading Span B = (Period high + Period low)/2 (52 Sessions)
    hi_val3 = df['High'].rolling(window = 52).max()
    low_val3 = df['Low'].rolling(window = 52).min() 
    df['SpanB'] = ((hi_val3 + low_val3)/2)

    # Lagging Span = Price shifted back 26 periods
    df['Lagging'] = df['Close'].shift(-26)

    return df

Prueba de generación de cálculos para un archivo csv

try:
    print('Trabajando en:', 'A')
    new_df = get_stock_df_from_csv('A')
    new_df = add_daily_return_to_df(new_df)
    new_df = add_cum_return_to_df(new_df)
    new_df = add_bollinger_bands(new_df)
    new_df = add_Ichimoku(new_df)
    new_df.to_csv(PATH + 'A' + '.csv')
except Exception as ex:
    print(ex)

Realizar y añadir los cálculos a todos los archivos de los tickers o acciones

for x in tickers :
    try:
        print('Trabajando en:', x)
        new_df = get_stock_df_from_csv(x)
        new_df = add_daily_return_to_df(new_df)
        new_df = add_cum_return_to_df(new_df)
        new_df = add_bollinger_bands(new_df)
        new_df = add_Ichimoku(new_df)
        new_df.to_csv(PATH + x + '.csv')
    except Exception as ex:
            print(ex) ### Resultado: 

Se obtiene para cada stock en cada archivo csv, los valores del retorno diario, retorno acumulado desde la fecha inicial, el promedio móvil, banda superior e inferior, línea base, Span A, Span B y lagging.

3. Generación de las funciones para la creación de las gráficas de Bollinger Bands e Ichimoku. Portafolio_inversion_graficos.py

Gráficar las Bollinger bands

def plot_with_boll_bands(df, ticker):

    fig = go.Figure()

# Gráficar las velas con Plotly
    candle = go.Candlestick(x=df.index, open=df['Open'],
    high=df['High'], low=df['Low'],
    close=df['Close'], name="Candlestick")

# Gráficar las tres líneas calculadas
    upper_line = go.Scatter(x=df.index, y=df['upper_band'], 
    line=dict(color='rgba(250, 0, 0, 0.75)', 
    width=1), name="Upper Band")

    mid_line = go.Scatter(x=df.index, y=df['middle_band'], 
    line=dict(color='rgba(0, 0, 250, 0.75)', 
    width=0.7), name="Middle Band")

    lower_line = go.Scatter(x=df.index, y=df['lower_band'], 
    line=dict(color='rgba(0, 250, 0, 0.75)', 
    width=1), name="Lower Band")

# Agregar los cuatro gráficos en uno solo
    fig.add_trace(candle)
    fig.add_trace(upper_line)
    fig.add_trace(mid_line)
    fig.add_trace(lower_line)

# Dar titulos al gráfico y los ejes, así como adicionar un slider
    fig.update_xaxes(title="Date", rangeslider_visible=True)
    fig.update_yaxes(title="Price")

    fig.update_layout(title=ticker + " Bollinger Bands",
    height=1000, width=1800, showlegend=True)
    plot(fig)

Gráfica de Ishimoku

# Función para la asignación del color de la nube

def get_fill_color(label):
    if label >= 1:
        return 'rgba(0,250,0,0.4)'
    else:
        return 'rgba(250,0,0,0.4)'

# Función para la gráfica de Ishimoku

def get_Ichimoku(df):

    candle = go.Candlestick(x=df.index, open=df['Open'],
    high=df['High'], low=df["Low"], close=df['Close'], name="Candlestick")

    df1 = df.copy()
    fig = go.Figure()
    df['label'] = np.where(df['SpanA'] > df['SpanB'], 1, 0)
    df['group'] = df['label'].ne(df['label'].shift()).cumsum()

    df = df.groupby('group')

    dfs = []
    for name, data in df:
        dfs.append(data)

    for df in dfs:
        fig.add_traces(go.Scatter(x=df.index, y=df.SpanA,
        line=dict(color='rgba(0,0,0,0)')))

        fig.add_traces(go.Scatter(x=df.index, y=df.SpanB,
        line=dict(color='rgba(0,0,0,0)'),
        fill='tonexty',
        fillcolor=get_fill_color(df['label'].iloc[0])))

    baseline = go.Scatter(x=df1.index, y=df1['Baseline'], 
    line=dict(color='pink', width=2), name="Baseline")

    conversion = go.Scatter(x=df1.index, y=df1['Conversion'], 
    line=dict(color='black', width=1), name="Conversion")

    lagging = go.Scatter(x=df1.index, y=df1['Lagging'], 
    line=dict(color='purple', width=2), name="Lagging")

    span_a = go.Scatter(x=df1.index, y=df1['SpanA'], 
    line=dict(color='green', width=2, dash='dot'), name="Span A")

    span_b = go.Scatter(x=df1.index, y=df1['SpanB'], 
    line=dict(color='red', width=1, dash='dot'), name="Span B")

    fig.add_trace(candle)
    fig.add_trace(baseline)
    fig.add_trace(conversion)
    fig.add_trace(lagging)
    fig.add_trace(span_a)
    fig.add_trace(span_b)

    fig.update_layout(height=1000, width=1800, showlegend=True)

    plot(fig)

### Resultado:

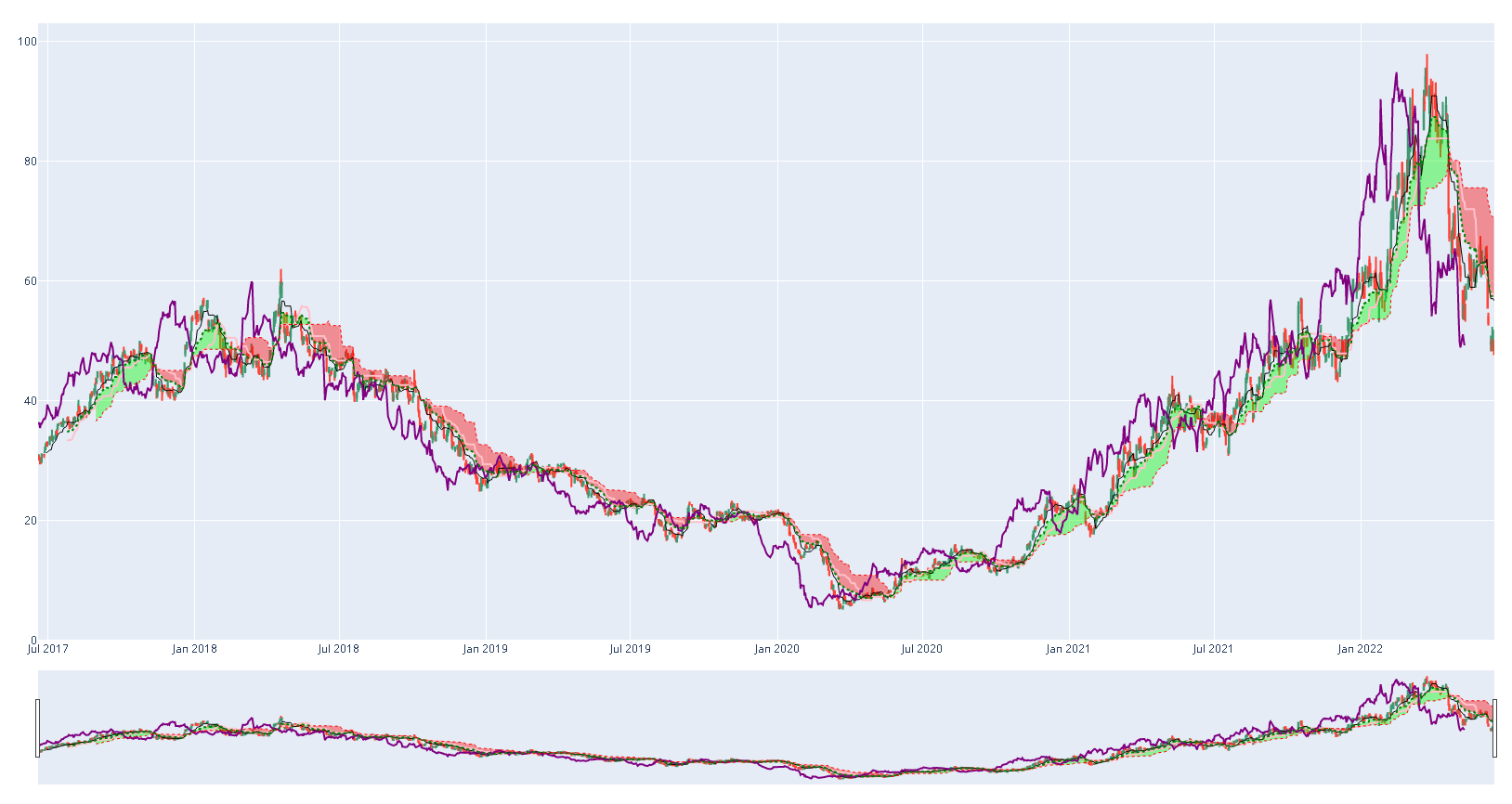
Gráfica de Bollinger Bands para el ticker AA.

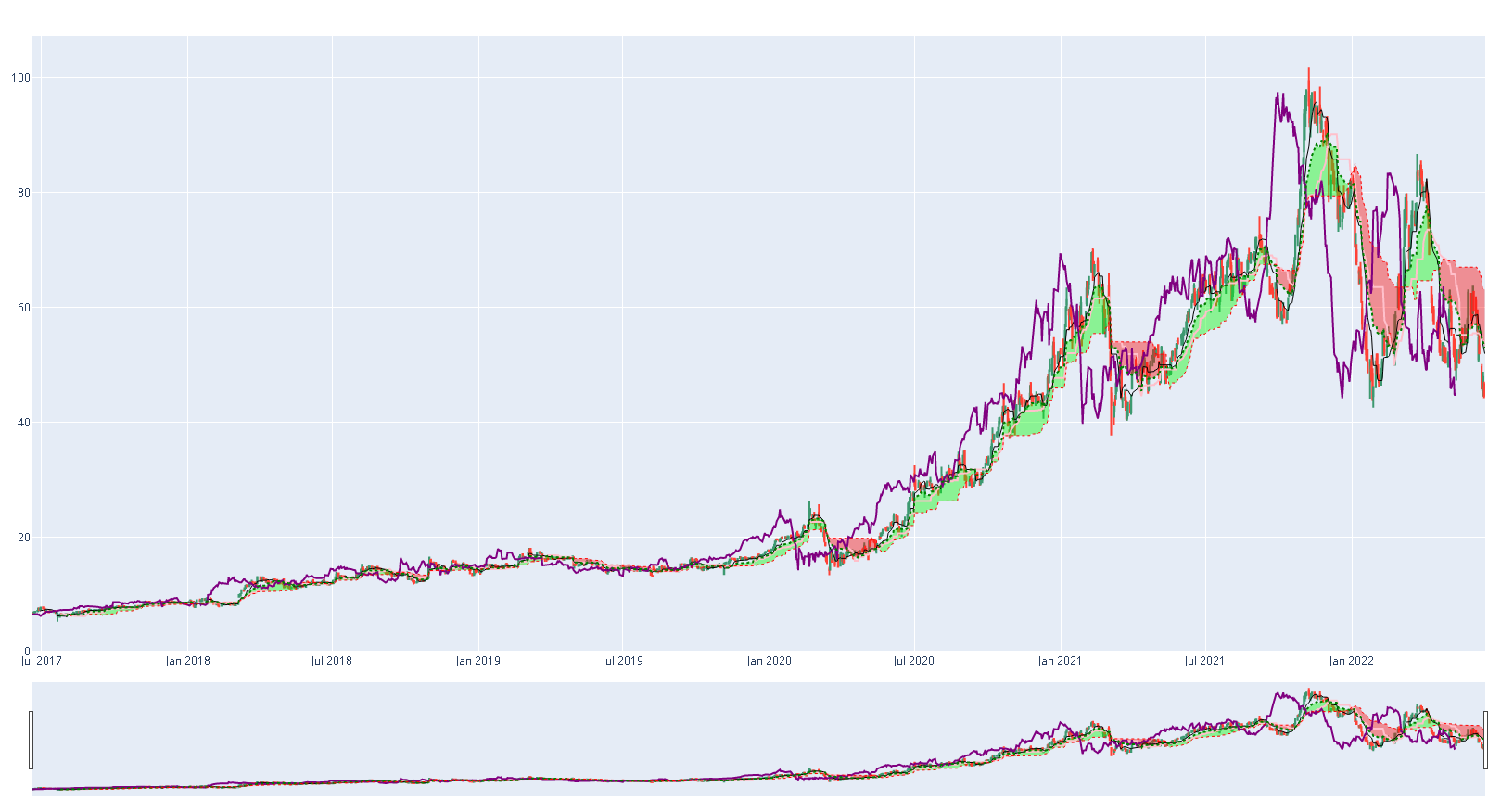
Gráfica Ishimoku para el ticker AA.

4. Obtener la información de los sectores para las acciones que conforman el Wilshire 5000. Portafolio_inversion_sectores.py

Esta información se encuentra en el archivo ‘big_stock_sectors.csv’

sec_df = pd.read_csv('E:\Estudio\Análisis de datos\Proyectos\Portafolio de inversión en python/big_stock_sectors.csv')

Separación en diferentes df de las acciones por sector

# Consulta de los sectores
print(sec_df['Sector'].unique())

"""
['Healthcare' 'Materials' 'SPAC' 'Discretionary' 'Real Estate'
 'Industrial' 'Financials' 'Information Technology' 'Industrials'
 'Staples' 'Services' 'Utilities' 'Communication' 'Energy' nan]
"""

indus_df = sec_df.loc[sec_df['Sector'] == 'Industrial']
health_df = sec_df.loc[sec_df['Sector'] == 'Healthcare']
it_df = sec_df.loc[sec_df['Sector'] == 'Information Technology']
comm_df = sec_df.loc[sec_df['Sector'] == 'Communication']
staple_df = sec_df.loc[sec_df['Sector'] == 'Staples']
discretion_df = sec_df.loc[sec_df['Sector'] == 'Discretionary']
materials_df = sec_df.loc[sec_df['Sector'] == 'Materials']
spac_df = sec_df.loc[sec_df['Sector'] == 'SPAC']
real_estate_df = sec_df.loc[sec_df['Sector'] == 'Real Estate']
financials_df = sec_df.loc[sec_df['Sector'] == 'Financials']
industrials_df = sec_df.loc[sec_df['Sector'] == 'Industrials']
services_df = sec_df.loc[sec_df['Sector'] == 'Services']
utilities_df = sec_df.loc[sec_df['Sector'] == 'Utilities']
energy_df = sec_df.loc[sec_df['Sector'] == 'Energy']

Creación de función para el cálculo del retorno acumulado para cada una de las acciones

def get_cum_ret_for_stocks(stock_df):
    tickers = []
    cum_rets = []

    for index, row in stock_df.iterrows():
        df = get_stock_df_from_csv(row['Ticker'])
        if df is None:
            pass
        else:
            tickers.append(row['Ticker'])
            cum = df['cum_return'].iloc[-1]
            cum_rets.append(cum)
    return pd.DataFrame({'Ticker':tickers, 'CUM_RET':cum_rets})

Aplicación de la función para encontrar el acumulado de las acciones

Healthcare = get_cum_ret_for_stocks(health_df)
Materials = get_cum_ret_for_stocks(materials_df)
SPAC = get_cum_ret_for_stocks(spac_df)
Discretionary = get_cum_ret_for_stocks(discretion_df)
Real_Estate = get_cum_ret_for_stocks(real_estate_df)
Industrial = get_cum_ret_for_stocks(indus_df)
Financials = get_cum_ret_for_stocks(financials_df)
IT = get_cum_ret_for_stocks(it_df)
Industrials = get_cum_ret_for_stocks(industrials_df)
Staples = get_cum_ret_for_stocks(staple_df)
Services = get_cum_ret_for_stocks(services_df)
Utilities = get_cum_ret_for_stocks(utilities_df)
Communication = get_cum_ret_for_stocks(comm_df)
Energy = get_cum_ret_for_stocks(energy_df)

Revisión por sector de las acciones con mayor rendimiento acumulado

print('Top 10 Industrial')
print(Industrial.sort_values(by=['CUM_RET'], ascending=False).head(10))

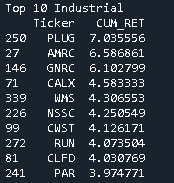
Acciones seleccionadas por mayor retorno acumulado: PLUG, AMRC, GNRC

Gráficar alguna de las acciones para decidir en cual se podría llegar a invertir.

df_ind = get_stock_df_from_csv('AMRC')
get_Ichimoku(df_ind)

    print('Top 10 Materials')
    print(Materials.sort_values(by=['CUM_RET'], ascending=False).head(10))

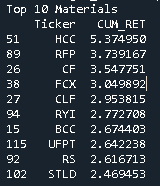
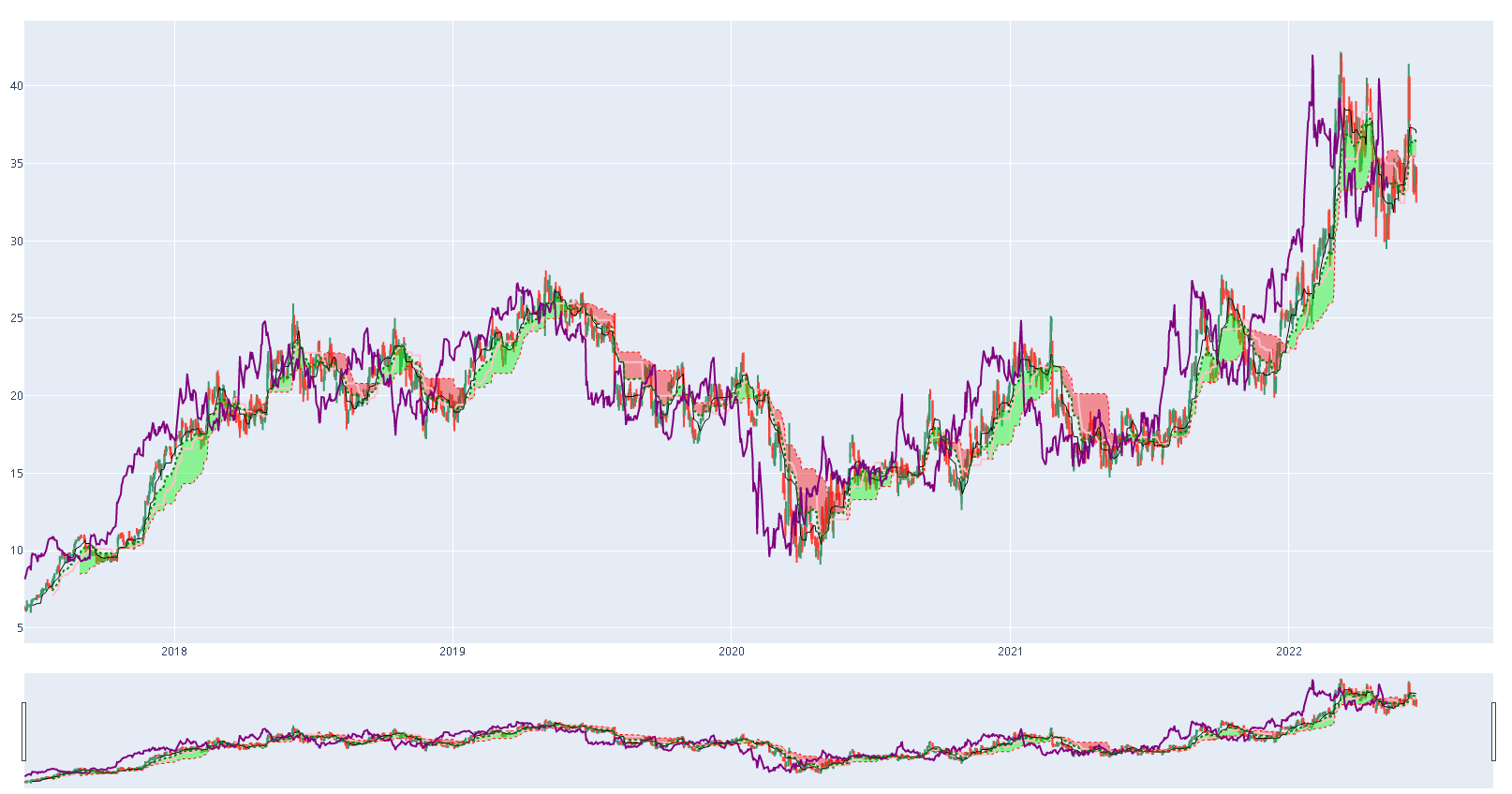
Acciones seleccionadas por mayor retorno acumulado: HCC, RFP, CF

Gráficar alguna de las acciones para decidir en cual se podría llegar a invertir.

    df_mat = get_stock_df_from_csv('HCC')
    get_Ichimoku(df_mat)

    print('Top 10 Discretionary')
    print(Discretionary.sort_values(by=['CUM_RET'], ascending=False).head(10))

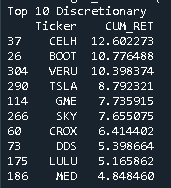
Acciones seleccionadas por mayor retorno acumulado: CELH, BOOT, VERU

Gráficar alguna de las acciones para decidir en cual se podría llegar a invertir.

    df_Discretionary = get_stock_df_from_csv('CELH')
    get_Ichimoku(df_Discretionary)

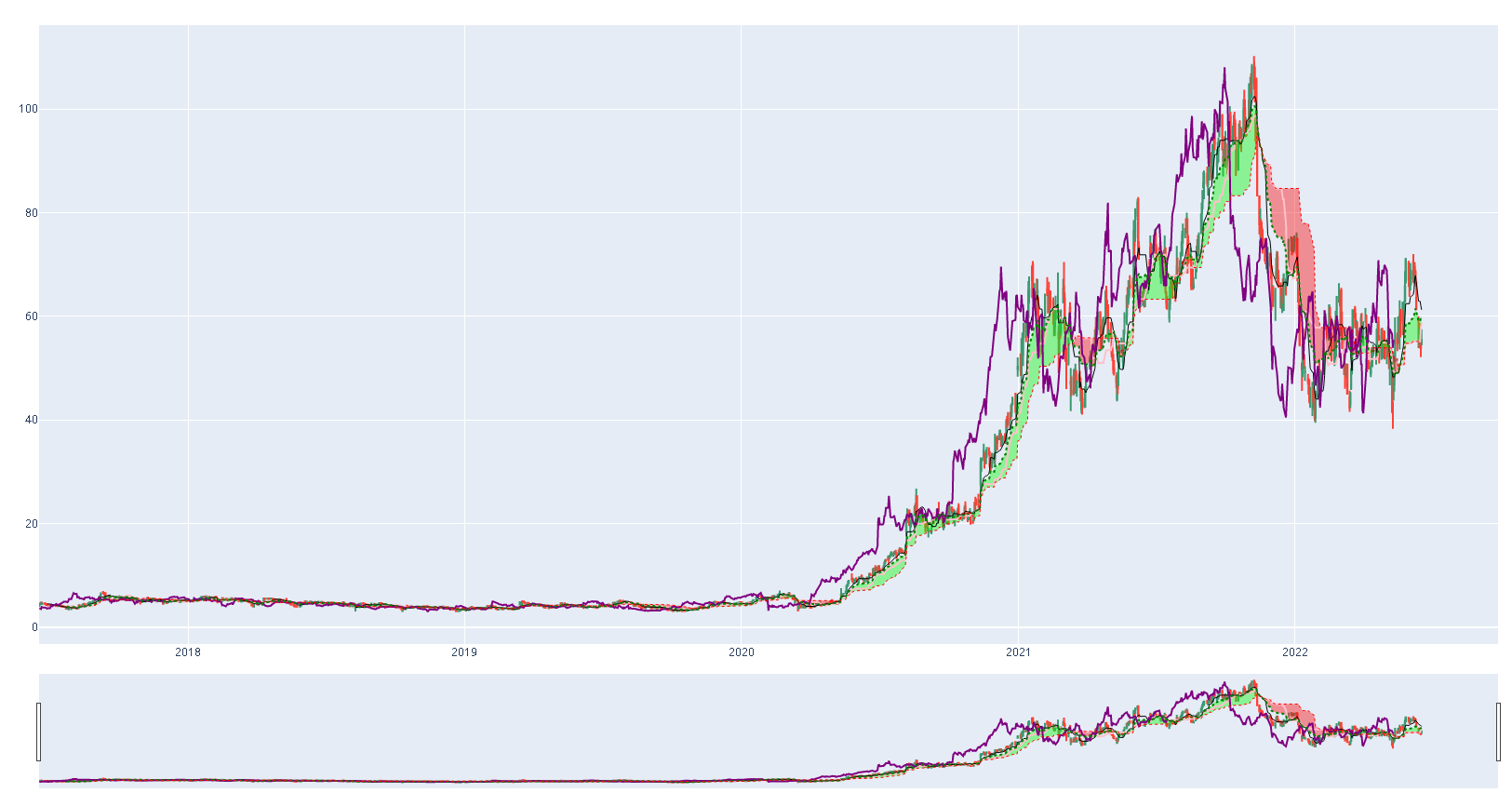
De esta manera se obtienen los retornos acumulados de las acciones por sector y se generan las gráficas de Ishimoku, con el fin de realizar una selección manual de las acciones que conformarán el portafolio.

5. Obtención del portafolio a invertir según la optimización de Markowitz con acciones con baja correlación. Portafolio_inversion_portafolio.py

Obtener los datos de los CSV creados

    def get_stock_df_from_csv(ticker):
        try:
            df = pd.read_csv(PATH + ticker + '.csv', index_col=0)
        except FileNotFoundError:
            print('El archivo no existe')
        else:
            return df

Unir en un único df múltiples acciones por el nombre de la columna

    def merge_df_by_column_name(col_name, sdate, edate, *tickers):
        # Will hold data for all dataframes with the same column name
        mult_df = pd.DataFrame()

        for x in tickers:
            df = get_stock_df_from_csv(x)
            mask = (df.index >= sdate) & (df.index <= edate)
            mult_df[x] = df.loc[mask][col_name]

        return mult_df

Optimización Markowitz del portafolio

Harry Markowitz proved that you could make what is called an efficient portfolio. That is a portfolio that optimizes return while also minimizing risk. We don’t benefit from analyzing individual securities at the same rate as if we instead considered a portfolio of stocks.

We do this by creating portfolios with stocks that are not correlated. We want to calculate expected returns by analyzing the returns of each stock multiplied by its weight.

w1r1 + w2r2 = rp

The standard deviation of the portfolio is found this way. Sum multiple calculations starting by finding the product of the first securities weight squared times its standard deviation squared. The middle is 2 times the correlation coefficient between the stocks. And, finally add those to the weight squared times the standard deviation squared for the second security.

(w1d1 + w2d2)^2 = w1^2*d1^2 + 2w1d1w2d2 + w2^2 * d2^2

Trazar la frontera más eficiente Selección de un portafolio con acciones previamente estudidas, con los datos del rendimiento acumulado e Ishimoku Para el caso seleccioné algunas de sectores epecíficos.

    port_list = ['PLUG', 'AMRC', 'GNRC',
    'HCC', 'RFP', 'CF',
    'IIPR', 'BRT', 'BRG',
    'CDNA', 'ZYXI', 'ARWR',
    'ATLC', 'KNSL', 'LPLA',
    'ENPH', 'APPS', 'SEDG',
    'RCMT', 'FCN', 'MHH',
    'NEE', 'MSEX', 'EXC',
    'TTGT', 'ROKU', 'IRDM',
    'OAS', 'VTNR', 'EGY']

    num_stocks = len(port_list)
    print(num_stocks)

Generar un df con los precios de cierre de todas las acciones seleccionadas

    mult_df = merge_df_by_column_name('Close', S_DATE, E_DATE, *port_list)

Generar un gráfico para los precios de las acciones

    fig = px.line(mult_df, x = mult_df.index, y = mult_df.columns)
    fig.update_layout(height=1000, width=1800, showlegend=True)
    fig.update_xaxes(title="Date", rangeslider_visible=True)
    fig.update_yaxes(title="Price")
    plot(fig)

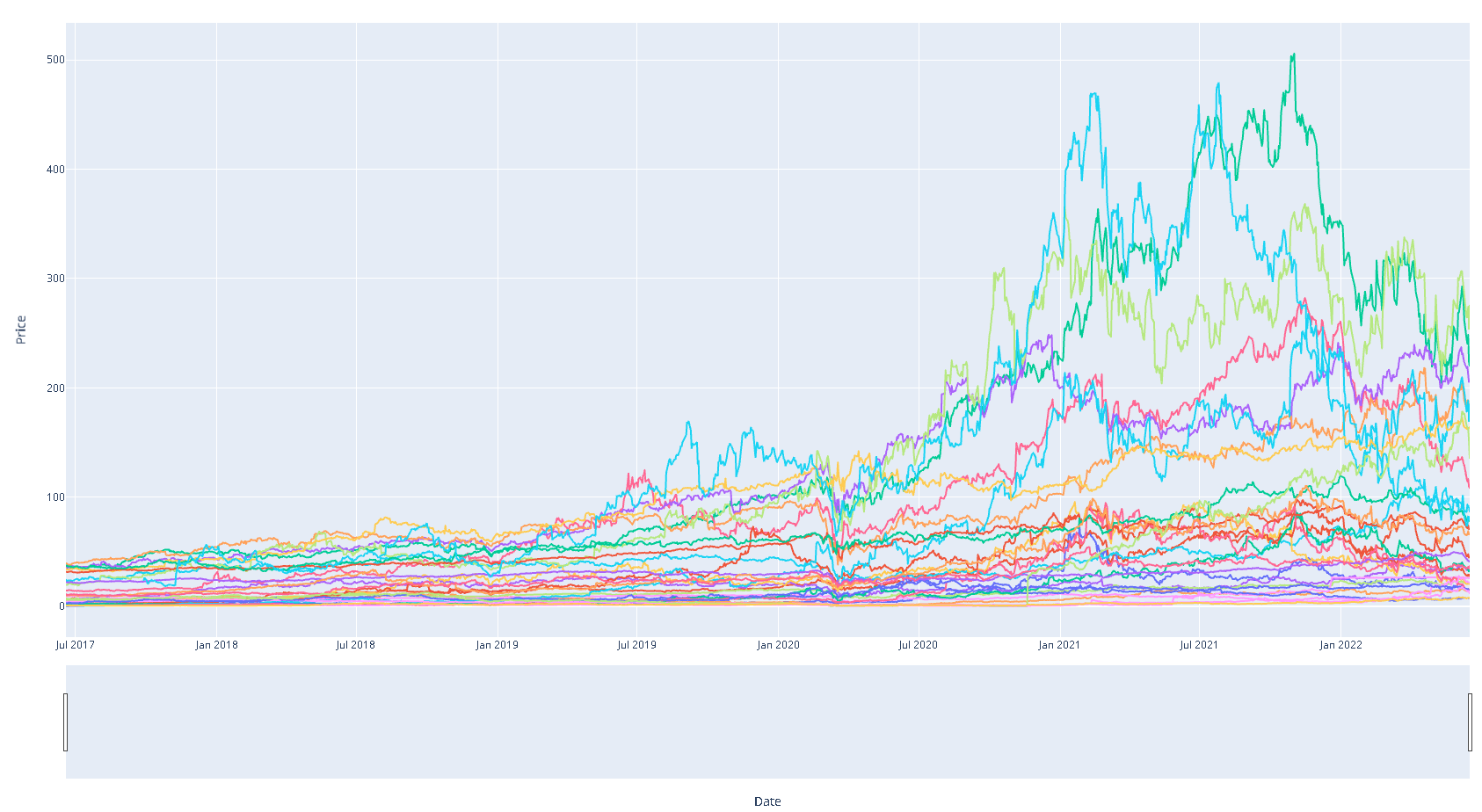
Generar una tranformación del precio y gráficar

    mult_df_t = np.log10(mult_df)

    fig = px.line(mult_df_t, x = mult_df_t.index, y = mult_df_t.columns)
    fig.update_layout(height=1000, width=1800, showlegend=True)
    fig.update_xaxes(title="Date", rangeslider_visible=True)
    fig.update_yaxes(title="Log10 Price")
    plot(fig)

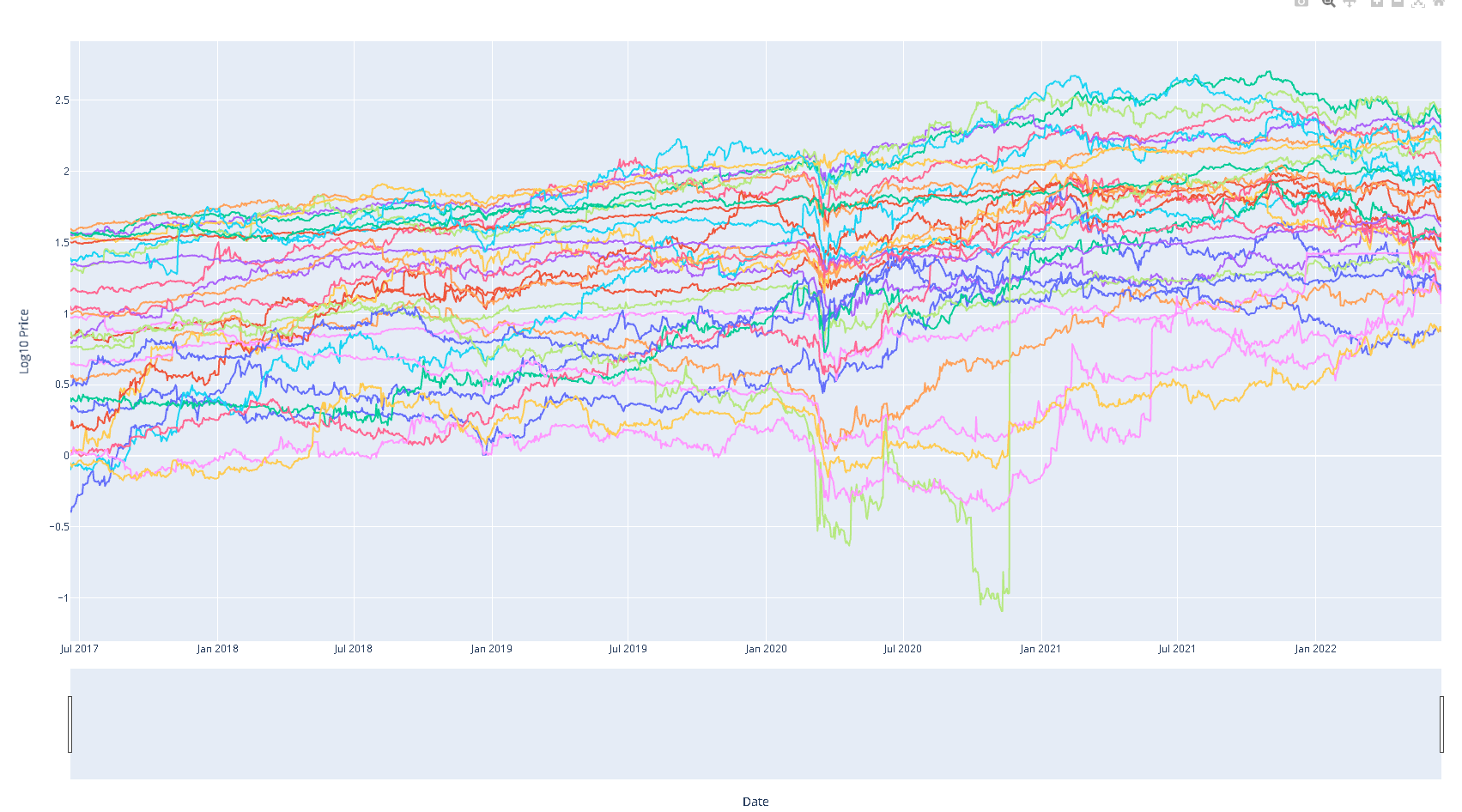
Retornos medios para un año (252 días hábiles)

    returns = np.log(mult_df / mult_df.shift(1))
    mean_ret = returns.mean()*252
    print(mean_ret)

Cálculo de la correlación de las acciones

    returns.corr()

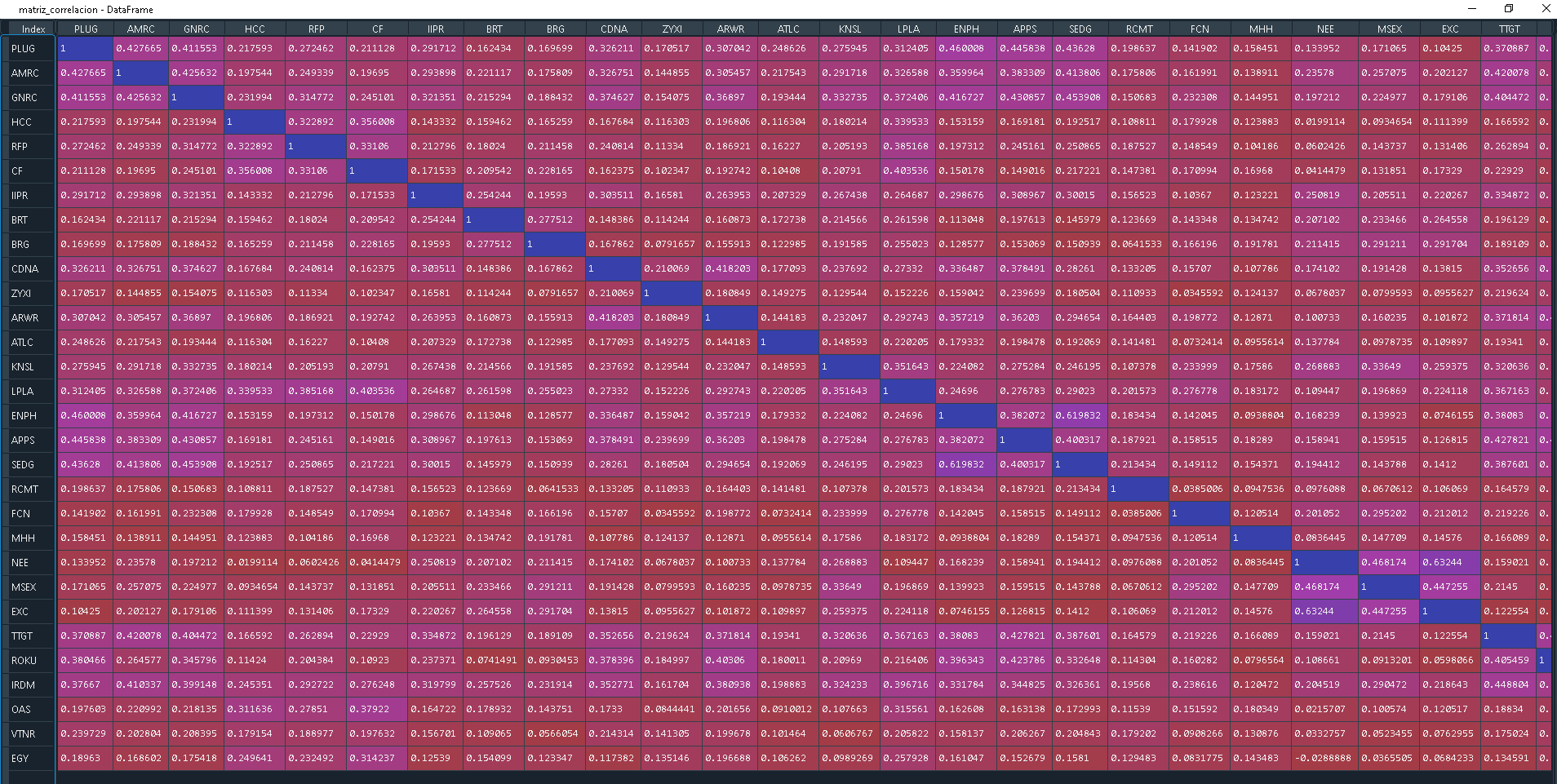
Gráfico de la correlación de las acciones Queremos un portafolio con baja correlación entre las acciones

    import seaborn as sns
    matriz_correlacion = returns.corr(method='spearman')
    fig = sns.heatmap(matriz_correlacion, annot=False)
    # fig.update_layout(height=1000, width=1800, showlegend=True)
    plt.show()

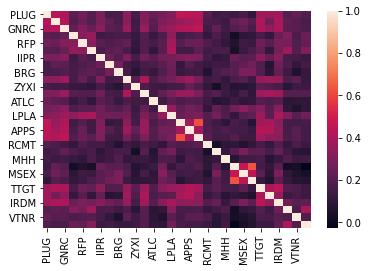
Generación de pesos aleatorios cuya suma es uno

    weights = np.random.random(num_stocks)
    weights /= np.sum(weights)  # weights = weights / np.sum(weights)
    print('Weights: ', weights)
    print('Total weight: ', np.sum(weights))

Cálculo del retorno promedio anual con los pesos aleatorios

    print(np.sum(weights * returns.mean()) * 252)

Cálculo de la volatilidad

    # Riesgo del portafolio con los pesos actuales

    print(np.sqrt(np.dot(weights.T, np.dot(returns.cov() * 252, weights))))

Ejecución de una simulación de 10000 portafolios mediante una función

    p_ret = [] # Retornos lista
    p_vol = [] # Volatilidad lista
    p_SR = [] # Sharpe Ratio lista
    p_wt = [] # Pesos por portafolio lista


    for x in range(10000):
        # Generar pesos aleatorios
        p_weights = np.random.random(num_stocks)
        p_weights /= np.sum(p_weights)

Calculo del retonrno según los pesos

ret_1 = np.sum(p_weights * returns.mean()) * 252
p_ret.append(ret_1)

Cálculo de la volatilidad

vol_1 = np.sqrt(np.dot(p_weights.T, np.dot(returns.cov() * 252, p_weights)))
p_vol.append(vol_1)

Cálculo del Sharpe ratio

SR_1 = (ret_1 - risk_free_rate) / vol_1
p_SR.append(SR_1)

Almacenar los pesos para cada portafolio

p_wt.append(p_weights)

Convertir a arreglos de Numpy

    p_ret = np.array(p_ret)
    p_vol = np.array(p_vol)
    p_SR = np.array(p_SR)
    p_wt = np.array(p_wt)

    p_ret, p_vol, p_SR, p_wt

Gráfica de los portafolios simulados o frontera más eficiente

    ports = pd.DataFrame({'Returns': p_ret, 'Volatility': p_vol, })
    ports.plot(x='Volatility', y = 'Returns', kind = 'scatter', figsize = (19,9))

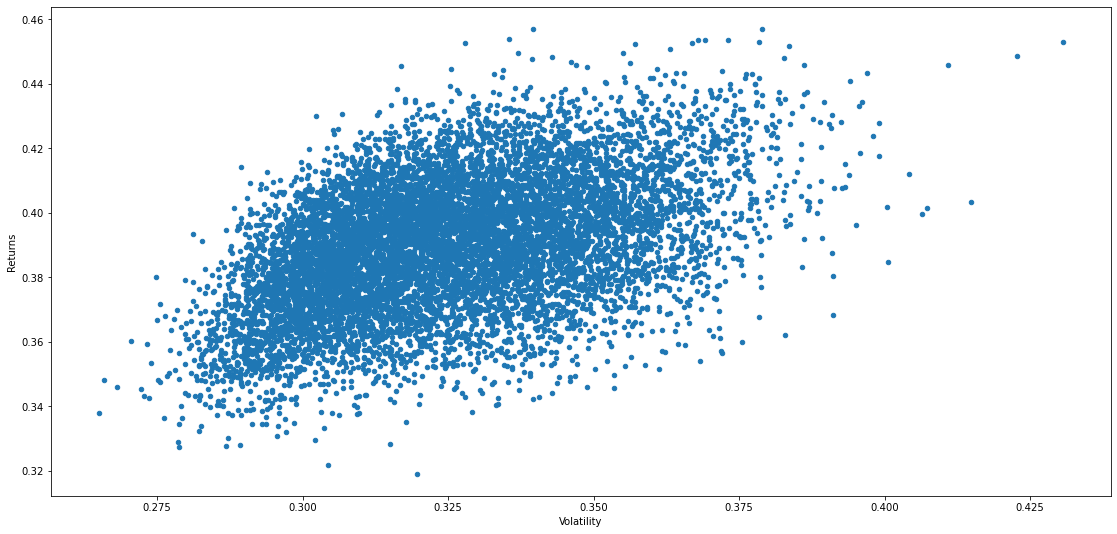
Sharpe ratio

People want to maximize returns while avoiding as much risk as possible. William Sharpe created the Sharpe Ratio to find the portfolio that provides the best return for the lowest amount of risk.

As return increases so does the Sharpe Ratio, but as Standard Deviation increase the Sharpe Ration decreases.

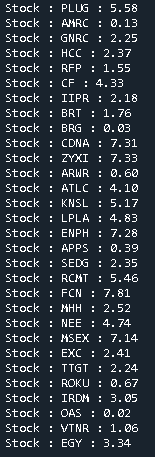
Devuelve el indice para el Sharpe Ratio más alto

    SR_idx = np.argmax(p_SR)

Encuentra los pesos ideales para el portafolio en ese index

    i = 0
    while i < num_stocks:
        print("Stock : %s : %2.2f" % (port_list[i], (p_wt[SR_idx][i] * 100)))
        i += 1

Encuentra la volatilidad de ese portafolio

    print("\nVolatility :", p_vol[SR_idx] * 100)

Encuentra el retorno de ese portafolio

    print("Return :", p_ret[SR_idx] * 100)

Resultado:

Listado de las acciones que conforman el portafolio, con las distribución porcentual según el mejor resultado obtenido trás la ejecucion de 10000 simulaciones.

Obtención de la volatilidad y el retorno esperado durante un año de inversión.

Se puede támbien tomar los porcenatjes menores a uno y acercarlos a uno, después calcular el portafolio. En situaciones en las que los porcentajes son menores a uno, lo que se puede hacer es acercarlos a uno o a una acción, o directamente desecharlos